Tuesday 23 July 2013
Monday 22 July 2013
PROVING CONVERSE OF BPT THEORM
Statement
If a line divides any two sides of a triangle (Δ) in the same ratio, then the line must be parallel (||) to the third side.
Given
In ΔABC, D and E are the two points of AB and AC respectively,
such that, AD/DB = AE/EC.
To Prove
DE || BC
Proof
In ΔABC,
given, AD/DB = AE/EC ----- (1)
Let us assume that in ΔABC, the point F is an intersect on the side AC.
So we can apply the Thales Theorem, AD/DB = AF/FC ----- (2)
Simplify, in (1) and (2) ==> AE/EC = AF/FC
Add 1 on both sides, ==> (AE/EC) + 1 = (AF/FC) + 1
==> (AE+EC)/EC = (AF+FC)/FC
==> AC/EC = AC/FC
==> EC = FC
From the above, we can say that the points E and F coincide on AC.
i.e., DF coincides with DE.
Since DF is parallel to BC, DE is also parallel BC
Hence the Converse of Basic Proportionality theorem is proved.
SOURCE- EASYCALCULATION.COM
If a line divides any two sides of a triangle (Δ) in the same ratio, then the line must be parallel (||) to the third side.
Given
In ΔABC, D and E are the two points of AB and AC respectively,
such that, AD/DB = AE/EC.
To Prove
DE || BC
Proof
In ΔABC,
given, AD/DB = AE/EC ----- (1)
Let us assume that in ΔABC, the point F is an intersect on the side AC.
So we can apply the Thales Theorem, AD/DB = AF/FC ----- (2)
Simplify, in (1) and (2) ==> AE/EC = AF/FC
Add 1 on both sides, ==> (AE/EC) + 1 = (AF/FC) + 1
==> (AE+EC)/EC = (AF+FC)/FC
==> AC/EC = AC/FC
==> EC = FC
From the above, we can say that the points E and F coincide on AC.
i.e., DF coincides with DE.
Since DF is parallel to BC, DE is also parallel BC
Hence the Converse of Basic Proportionality theorem is proved.
SOURCE- EASYCALCULATION.COM
Sunday 21 July 2013
similarity in triangles
Two geometrical objects are called similar if they both have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or shrinking), possibly with additional translation, rotation and reflection.
This means that either object can be rescaled, repositioned, and
reflected, so as to coincide precisely with the other object. If two
objects are similar, each is congruent to the result of a uniform scaling of the other.
If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure.
This article assumes that a scaling can have a scale factor of 1, so that all congruent shapes are also similar, but some school text books specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different to qualify as similar.
 and
and 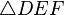 are said to be similar if either of the following equivalent conditions holds:
are said to be similar if either of the following equivalent conditions holds:
1. They have two identical angles, which implies that their angles are all identical. For instance:
 and
and 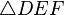 are similar, one writes
are similar, one writes
If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure.
This article assumes that a scaling can have a scale factor of 1, so that all congruent shapes are also similar, but some school text books specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different to qualify as similar.
 | |
| figures with same colours are similar |
Similar triangles
Two triangles and
and 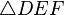 are said to be similar if either of the following equivalent conditions holds:
are said to be similar if either of the following equivalent conditions holds:1. They have two identical angles, which implies that their angles are all identical. For instance:
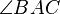 is equal in measure to
is equal in measure to 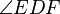 , and
, and  is equal in measure to
is equal in measure to  . This also implies that
. This also implies that  is equal in measure to
is equal in measure to 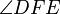 .
.
 . This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other.
. This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other.
 and
and  is equal in measure to
is equal in measure to  .
.
 and
and 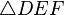 are similar, one writes
are similar, one writesSaturday 13 July 2013
OGIVES
Cumulative histograms, also known as ogives, are graphs that can be used to determine how many data values lie above or below a particular value in a data set. The cumulative frequency is calculated from a frequency table, by adding each frequency to the total of the frequencies of all data values before it in the data set. The last value for the cumulative frequency will always be equal to the total number of data values, since all frequencies will already have been added to the previous total.
An ogive is drawn by
- plotting the beginning of the first interval at a
 -value of zero;
-value of zero; - plotting the end of every interval at the
 -value equal to the cumulative count for that interval; and
-value equal to the cumulative count for that interval; and - connecting the points on the plot with straight lines.
Example 1: Cumulative frequencies and ogives
Determine the cumulative frequencies of the following grouped data and complete the table below. Use the table to draw an ogive of the data.
| Interval | Frequency | Cumulative frequency |
 | 5 | |
 | 7 | |
 | 12 | |
 | 10 | |
 | 6 |
Solution
To determine the cumulative frequency, we add up the frequencies going down the table. The first cumulative frequency is just the same as the frequency, because we are adding it to zero. The final cumulative frequency is always equal to the sum of all the frequencies. This gives the following table:
| Interval | Frequency | Cumulative frequency |
 | 5 | 5 |
 | 7 | 12 |
 | 12 | 24 |
 | 10 | 34 |
 | 6 | 40 |
The first coordinate in the plot always starts at a  -value of 0 because we always start from a count of zero. So, the first coordinate is at
-value of 0 because we always start from a count of zero. So, the first coordinate is at  — at the beginning of the first interval. The second coordinate is at the end of the first interval (which is also the beginning of the second interval) and at the first cumulative count, so
— at the beginning of the first interval. The second coordinate is at the end of the first interval (which is also the beginning of the second interval) and at the first cumulative count, so  . The third coordinate is at the end of the second interval and at the second cumulative count, namely
. The third coordinate is at the end of the second interval and at the second cumulative count, namely  , and so on.
, and so on.
 -value of 0 because we always start from a count of zero. So, the first coordinate is at
-value of 0 because we always start from a count of zero. So, the first coordinate is at  — at the beginning of the first interval. The second coordinate is at the end of the first interval (which is also the beginning of the second interval) and at the first cumulative count, so
— at the beginning of the first interval. The second coordinate is at the end of the first interval (which is also the beginning of the second interval) and at the first cumulative count, so  . The third coordinate is at the end of the second interval and at the second cumulative count, namely
. The third coordinate is at the end of the second interval and at the second cumulative count, namely  , and so on.
, and so on.
Computing all the coordinates and connecting them with straight lines gives the following ogive.
Ogives do look similar to frequency polygons, which we saw earlier. The most important difference between them is that an ogive is a plot of cumulative values, whereas a frequency polygon is a plot of the values themselves. So, to get from a frequency polygon to an ogive, we would add up the counts as we move from left to right in the graph.
Ogives are useful for determining the median, percentiles and five number summary of data. Remember that the median is simply the value in the middle when we order the data. A quartile is simply a quarter of the way from the beginning or the end of an ordered data set. With an ogive we already know how many data values are above or below a certain point, so it is easy to find the middle or a quarter of the data set.
source- m.everythingmaths.co.za
Sunday 7 July 2013
STATISTICS (MODE AND MEAN)
MODE
L is the lower class limit of modal class
When individual series or discrete series are given then mode is the most frequently occuring observation.But when continuous series are given then we have to take out the average mode that is
mode = L + [(f1-f0) / (2f1-f0-f2)] x h
where:
f0 is the frequency previous to the model class
f1 is the Frequency of the model class
f2 is the frequency next to the model class
h is the size of model class i.e. difference between upper
and lower class boundaries of model class.
Model class is a class with the maximum frequency.
MEDIANSame is the case when we have to find median.There are different methods to find median in different series.When individual or discrete series are given then
if no. of observations are odd then
median = (n+1/2)th observations.
if no. of observations are even then
median=mean of (n/2)th and (n/2÷1)th observations.
When continuous series are given then
median= L+(n/2-c.f.÷f) ×h
Thursday 4 July 2013
STATISTICS OVERVIEW (MEAN)
THERE ARE THREE TYPES OF SERIES-
1.INDIVIDUAL SERIES
- Let x1, x2.....................xn be given obs. and 'n' be the total no. of obs.,then
mean = Σxi/n
1.INDIVIDUAL SERIES
- Let x1, x2.....................xn be given obs. and 'n' be the total no. of obs.,then
mean = Σxi/n
where xi is sum of all obs.
2.DISCRETE SERIES
- Let x1,x2..........xn be given obs. and f1,f2.....fn be their frequencies then
mean= Σfixi/Σfi
3.CONTINUOUS SERIES
- Continuous series means when class intervals are given.
Mean can be found by three methods here-
(A)DIRECT METHOD
When upper and lower limits of the class intervals are small.
mean=Σfixi/Σfi
(B)DEVIATION OR ASSUMED MEAN METHOD
When upper and lower limits of the class intervals are large,then this method is used.
the assumed mean is taken from class mark(xi)
mean= A + Σfidi/Σfi, where d = mean – A, where A is the assumed mean.
(C)STEP DEVIATION METHOD
This method is used to make the calculations for finding the mean easy.
Mean= A + (Σfiui/Σfi)h, where A is the assumed mean and u = di/h.
NOTE- Step Deviation method is used mainly for finding the mean when data is given in the continuous series with large value of upper and lower limits.We can use the other two methods if they are specified in the question or according to the conditions of the questions.
Subscribe to:
Posts (Atom)

