Two geometrical objects are called similar if they both have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or shrinking), possibly with additional translation, rotation and reflection.
This means that either object can be rescaled, repositioned, and
reflected, so as to coincide precisely with the other object. If two
objects are similar, each is congruent to the result of a uniform scaling of the other.
If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure.
This article assumes that a scaling can have a scale factor of 1, so that all congruent shapes are also similar, but some school text books specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different to qualify as similar.
 and
and 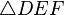 are said to be similar if either of the following equivalent conditions holds:
are said to be similar if either of the following equivalent conditions holds:
1. They have two identical angles, which implies that their angles are all identical. For instance:
 and
and 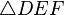 are similar, one writes
are similar, one writes
If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure.
This article assumes that a scaling can have a scale factor of 1, so that all congruent shapes are also similar, but some school text books specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different to qualify as similar.
 | |
| figures with same colours are similar |
Similar triangles
Two triangles and
and 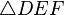 are said to be similar if either of the following equivalent conditions holds:
are said to be similar if either of the following equivalent conditions holds:1. They have two identical angles, which implies that their angles are all identical. For instance:
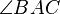 is equal in measure to
is equal in measure to 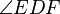 , and
, and  is equal in measure to
is equal in measure to  . This also implies that
. This also implies that  is equal in measure to
is equal in measure to 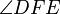 .
.
 . This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other.
. This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other.
 and
and  is equal in measure to
is equal in measure to  .
.
 and
and 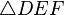 are similar, one writes
are similar, one writes

No comments:
Post a Comment