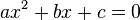Arithematic progression

METHODS TO SOLVE QUADRATIC EQUATIONS

The solution of a quadratic equation is the value of x when you set the equation equal to zero
i.e. When you solve the following general equation:  ax² + bx + c=0

Given a quadratic equation: ax ² + bx + c=0

 There are three methods to solve a quadratic equation-

First ------- Factorisation

General Steps to solve by factoring

•  Create a factor chart for all factor pairs of c
  • A factor pair is just two numbers that multiply and give you 'c'
• Out of all of the factor pairs from step 1, look for the pair (if it exists) that add up to b
• Insert the pair you found in step 2 into two binomial.
•  Solve each binomial for zero to get the solutions of the quadratic equation.

--Before learning next two steps we need to know that what is a discriminant??

       It is represented as D=b²-4ac

It decides the nature of the roots of the quadratic equation.

   -if D is greater than 0 then roots are real

   -if D is o then roots are same

   -if D is less than 0 then roots are not real.

Second----------Completing the squares
        General steps are-

•  Divide the whole equation by the coefficient of x ²  or 'a'

it becomes            ax ²/a + bx/a + c/a=0
                       or
                    x ² + bx/a + c/a=0

• Now add and subtract (b/2a) ² to L.H.S.

Third----------Quadratic formula

              General steps

•         Just apply the formula-

 

quadratic equations (introduction)

In elementary algebra, a quadratic equation (from the Latin quadratus for "square") is any equation having the form

where x represents an unknown, and a, b, and c are constants with a not equal to 0. If a = 0, then the equation is linear, not quadratic. The constants a, b, and c are called, respectively, the quadratic coefficient, the linear coefficient and the constant or free term.

source: youtube.com