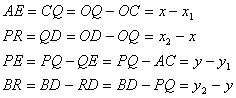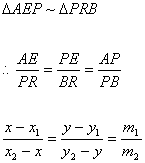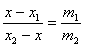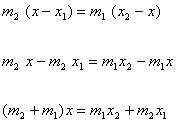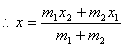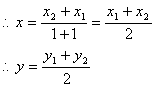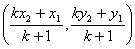formulas used in coordinate geometry

Distance between two points

Let P (x₁, y₁) and Q (x₂, y₂) be the two points. We have to find PQ.

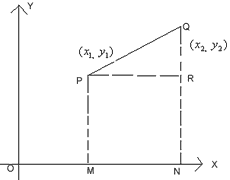
OM = x₁, PM = y₁ = RN

ON = x₂, QN = y₂

PR = MN = ON – OM

= x₂ – x₁

QR = QN – RN = y₂ – y₁

By Pythagoras theorem

PQ² = PR² + QR²

= (x₂ - x₁)² + (y₂ – y₁)²

If x₁ = 0, y₁ = 0, x₂ = x and y₂ = y

Then 

Section Formula

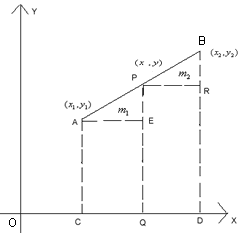
Let P (x, y) divided a line AB such that AP : PB = m₁ : m₂.

Let coordinates of A are (x₁, y₁) and B are (x₂, y₂).

It is obvious that

Taking, 

Similarity 

Note

(i) if P is mid point of AB, then AP : PB = 1 : 1

(ii) If m₁ : m₂ = k, then coordinates of P are 

coordinate geometry

SAMPLE QUESTIONS -ARITHMETIC PROGRESSIONS

1. An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th
term.
Solution: 12 = a + 2d
106 = a + 49d
So, 106-12 = 47d
Or, 94 = 47d
Or, d = 2
Hence, a = 8
And, n29 = 8 + 28x2 = 64

2. If the 3rd and the 9th terms of an AP are 4 and -8 respectively, which term of this AP is zero? 

Solution: -8 = a + 8d 

4 = a + 2d 

Or, -8 – 4 = 6d 

Or, -12 = 6d 

Or, d = -2 

Hence, a = -8 + 16 = 8 

0 = 8 + -2(n-1) 

Or, 8 = 2(n-1) 

Or, n-1 = 4 

3. The 17th term of an AP exceeds its 10th term by 7. Find the common difference. 

Solution: n7 = a + 6d 

And, n10 = a + 9d 

Or, a + 9d – a – 6d = 7 

Or, 3d = 7 

Or, d = 7/3

4. Which term of the AP: 3. 15, 27, 39, … will be 132 more than its 54th term? 

Solution: d = 12, 

132/12 = 11 

So, 54 + 11 = 65th term will be 132 more than the 54th term. 

5. How many three digit numbers are divisible by 7? 

Solution: Smallest three digit number divisible by 7 is 105 

Greatest three digit number divisible by 7 is 994 

Number of terms 

= {(last term – first term )/common difference }+1 

= {(994-105)/7}+1 

= (889/7)+1=127+1=128 

WWW.WEEBLY.COM<SOURCE>