Distance between two points
Let P (x1, y1) and Q (x2, y2) be the two points. We have to find PQ.
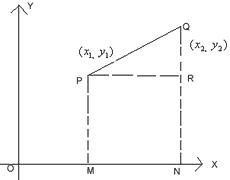
OM = x1, PM = y1 = RN
ON = x2, QN = y2PR = MN = ON – OM= x2 – x1QR = QN – RN = y2 – y1By Pythagoras theoremPQ2 = PR2 + QR2= (x2 - x1)2 + (y2 – y1)2If x1 = 0, y1 = 0, x2 = x and y2 = yThen
Section Formula
Let P (x, y) divided a line AB such that AP : PB = m1 : m2.
Let coordinates of A are (x1, y1) and B are (x2, y2).
It is obvious that
Taking,
SimilarityNote(i) if P is mid point of AB, then AP : PB = 1 : 1(ii) If m1 : m2 = k, then coordinates of P are
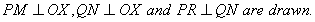
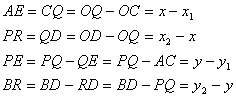
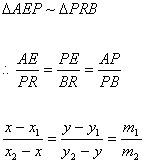
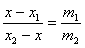
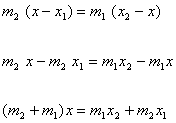
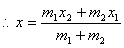
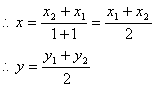
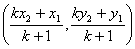
No comments:
Post a Comment