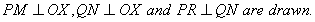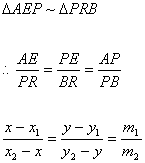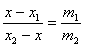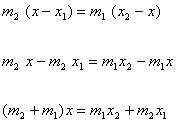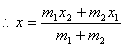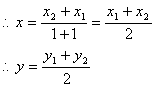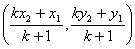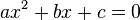Sunday, 22 December 2013
Wednesday, 11 December 2013
Sunday, 1 December 2013
Tuesday, 12 November 2013
formulas used in coordinate geometry
Distance between two points
Let P (x1, y1) and Q (x2, y2) be the two points. We have to find PQ.
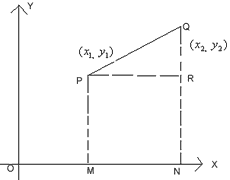
OM = x1, PM = y1 = RN
ON = x2, QN = y2PR = MN = ON – OM= x2 – x1QR = QN – RN = y2 – y1By Pythagoras theoremPQ2 = PR2 + QR2= (x2 - x1)2 + (y2 – y1)2If x1 = 0, y1 = 0, x2 = x and y2 = yThen
Section Formula
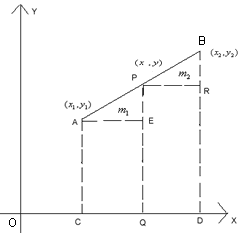
Let P (x, y) divided a line AB such that AP : PB = m1 : m2.
Let coordinates of A are (x1, y1) and B are (x2, y2).
It is obvious that
Taking,
SimilarityNote(i) if P is mid point of AB, then AP : PB = 1 : 1(ii) If m1 : m2 = k, then coordinates of P are
Saturday, 9 November 2013
Monday, 4 November 2013
SAMPLE QUESTIONS -ARITHMETIC PROGRESSIONS
1. An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th
term.
Solution: 12 = a + 2d
106 = a + 49d
So, 106-12 = 47d
Or, 94 = 47d
Or, d = 2
Hence, a = 8
And, n29 = 8 + 28x2 = 64
term.
Solution: 12 = a + 2d
106 = a + 49d
So, 106-12 = 47d
Or, 94 = 47d
Or, d = 2
Hence, a = 8
And, n29 = 8 + 28x2 = 64
2. If the 3rd and the 9th terms of an AP are 4 and -8 respectively, which term of this AP is zero?
Solution: -8 = a + 8d
4 = a + 2d
Or, -8 – 4 = 6d
Or, -12 = 6d
Or, d = -2
Hence, a = -8 + 16 = 8
0 = 8 + -2(n-1)
Or, 8 = 2(n-1)
Or, n-1 = 4
3. The 17th term of an AP exceeds its 10th term by 7. Find the common difference.
Solution: n7 = a + 6d
And, n10 = a + 9d
Or, a + 9d – a – 6d = 7
Or, 3d = 7
Or, d = 7/3
4. Which term of the AP: 3. 15, 27, 39, … will be 132 more than its 54th term?
Solution: d = 12,
132/12 = 11
So, 54 + 11 = 65th term will be 132 more than the 54th term.
5. How many three digit numbers are divisible by 7?
Solution: Smallest three digit number divisible by 7 is 105
Greatest three digit number divisible by 7 is 994
Number of terms
= {(last term – first term )/common difference }+1
= {(994-105)/7}+1
= (889/7)+1=127+1=128
WWW.WEEBLY.COM<SOURCE>
Tuesday, 22 October 2013
Saturday, 19 October 2013
METHODS TO SOLVE QUADRATIC EQUATIONS
The solution of a quadratic equation is the value of x when you set the equation equal to zero
i.e. When you solve the following general equation: ax² + bx + c=0
i.e. When you solve the following general equation: ax² + bx + c=0
Given a quadratic equation: ax ² + bx + c=0
There are three methods to solve a quadratic equation-
First ------- Factorisation
General Steps to solve by factoring
- Create a factor chart for all factor pairs of c
- A factor pair is just two numbers that multiply and give you 'c'
- Out of all of the factor pairs from step 1, look for the pair (if it exists) that add up to b
- Insert the pair you found in step 2 into two binomial.
- Solve each binomial for zero to get the solutions of the quadratic equation.
--Before learning next two steps we need to know that what is a discriminant??
It is represented as D=b²-4ac
It decides the nature of the roots of the quadratic equation.
-if D is greater than 0 then roots are real
-if D is o then roots are same
-if D is less than 0 then roots are not real.Second----------Completing the squares
General steps are-
- Divide the whole equation by the coefficient of x ² or 'a'
or
x ² + bx/a + c/a=0
- Now add and subtract (b/2a) ² to L.H.S.
General steps
- Just apply the formula-
Sunday, 6 October 2013
quadratic equations (introduction)
In elementary algebra, a quadratic equation (from the Latin quadratus for "square") is any equation having the form
source: youtube.com
Monday, 9 September 2013
THIS TIME GO FEARLESS TO CRACK YOUR MATHS EXAM!!
Many
students, even some really intelligent and talented ones, have a
strange enemy. They often find it difficult to finish the paper within
the allotted time. They are forced to leave a few questions just because
they run out of time and often it has been found that the questions
they leave are those which they otherwise could do very easily. It can
be very disappointing if you are forced to skip such easy questions.
But how can you avoid a situation like this? Many people suggest a single tablet for this "Time management". But how to manage time and how to stop it from running out is a difficult proposition, especially for an average 14-15-year-old tenth grader.
Here are certain tips by experts from to help you out to finish your paper well before time.
1. Understand your examThe most important thing is to understand the examination you are about to take. In the class X mathematics paper, there are 30 questions in four sections A, B, C and D and we have 180 minutes to answer these questions. Here, a rough calculation is that we get about six minutes to answer a question. But that is not the fact.
The question paper contains 'very short answer' type, 'short answer' type and 'long answer' type questions and the time requirement for each type is different. An ideal allotment for the four sections is as shown below:
Additionally,
you must practice the habit of finishing samples papers in 140-150
minutes. This will help you simulate and exercise examination pressures
better.
But how can you avoid a situation like this? Many people suggest a single tablet for this "Time management". But how to manage time and how to stop it from running out is a difficult proposition, especially for an average 14-15-year-old tenth grader.
Here are certain tips by experts from to help you out to finish your paper well before time.
1. Understand your examThe most important thing is to understand the examination you are about to take. In the class X mathematics paper, there are 30 questions in four sections A, B, C and D and we have 180 minutes to answer these questions. Here, a rough calculation is that we get about six minutes to answer a question. But that is not the fact.
The question paper contains 'very short answer' type, 'short answer' type and 'long answer' type questions and the time requirement for each type is different. An ideal allotment for the four sections is as shown below:
2. Use the first 15 minutes effectively
You
get a good 15 minutes in the beginning to read the question paper --
use this time to do just that, READ. Read all the 30 questions in 15
minutes. While reading, mark the questions into categories viz easy,
manageable and tough. This is done to have an overall idea about the
questions and make a rough plan.
3. Don't worry about the tough ones
The
moment you find that there are a few tough questions; it is natural
that you start worrying about them. This is not required and will only
harm your performance.
The
fact is that they may look a bit tough on the surface, but when you
actually work on them you will find most of them to be much easier than
they seemed. So be happy about the easy ones and don't get unduly
worried about the tougher lot.
4. Prioritise your attempt
Always
attempt the easy questions first and then move on to the manageable
ones and ensure that you complete them before taking on the difficult
ones. This will ensure that you are not leaving any question that you
know.
Once you successfully attempt all the easy and manageable questions, your confidence will grow and you will be
mentally ready to take on the more challenging questions.
5. Ensure speed and accuracy
Use
quicker methods in calculations to ensure that you are not wasting time
and your answers are correct. Mostly, we take a lot of time to solve a
problem if we happen to make some error in the process.
For
example, if you make an error in the sign of a term (+/-), you may not
be able to solve questions involving quadratic equations or linear
equations. Therefore avoiding silly mistakes is very important to save time.
6. Keep an eye on your watch
Keeping
an eye on your watch is of course not to increase your stress. This is
just to see that you are broadly adhering to the time allocation we
discussed in the beginning. A minor variation is not at all a reason to
worry.
7. Avoid thinking too much about a questionThinking
about the questions before you attempt them is essential; but not to
such an extent that you waste a lot of time on one question.
Also
you need not write a very lengthy answer to a question just because the
question is easy and you know it very well. Remember, you need to just
answer the question and nothing more. Any over-attempt will be a mere
waste of time.
Sunday, 8 September 2013
TRIGNOMETRY-solve these.
QUESTIONS
ANSWERS
Area = (1/2)x2 = 50 , solve for x: x = 10
We now use Pythagoras to find H: x2 + x2 = H2
Solve for H: H = 10 sqrt(2)
tan(A) = opposite side / adjacent side = a/b = 3/4
We can say that: a = 3k and b = 4k , where k is a coefficient of proportionality. Let us find h.
Pythagoras theorem: h2 = (3k)2 + (5k)2
Solve for h: h = 5k
sin(A) = a / h = 3k / 5k = 3/5 and cos(A) = 4k / 5k = 4/5
sin(B) = b/h and cos(B) = c/h
sin(B) = cos(B) means b/h = c/h which gives c = b
The two sides are equal in length means that the triangle is isosceles and angles B and C are equal in size of 45o.
tan(x) = 5/2.5 = 2 , x = arctan(2)
larger angle made by diagonals 2x = 2 arctan(2) = 127o (3 significant digits)
Smaller angle made by diagonals 180 - 2x = 53o.

122 = 82 + x2 - 2*8*x*cos(59o)
Solve the quadratic equation for x: x = 14.0 and x = -5.7
x cannot be negative and therefore the solution is x = 14.0 (rounded to one decimal place).
Friday, 2 August 2013
Tuesday, 23 July 2013
Monday, 22 July 2013
PROVING CONVERSE OF BPT THEORM
Statement
If a line divides any two sides of a triangle (Δ) in the same ratio, then the line must be parallel (||) to the third side.
Given
In ΔABC, D and E are the two points of AB and AC respectively,
such that, AD/DB = AE/EC.
To Prove
DE || BC
Proof
In ΔABC,
given, AD/DB = AE/EC ----- (1)
Let us assume that in ΔABC, the point F is an intersect on the side AC.
So we can apply the Thales Theorem, AD/DB = AF/FC ----- (2)
Simplify, in (1) and (2) ==> AE/EC = AF/FC
Add 1 on both sides, ==> (AE/EC) + 1 = (AF/FC) + 1
==> (AE+EC)/EC = (AF+FC)/FC
==> AC/EC = AC/FC
==> EC = FC
From the above, we can say that the points E and F coincide on AC.
i.e., DF coincides with DE.
Since DF is parallel to BC, DE is also parallel BC
Hence the Converse of Basic Proportionality theorem is proved.
SOURCE- EASYCALCULATION.COM
If a line divides any two sides of a triangle (Δ) in the same ratio, then the line must be parallel (||) to the third side.
Given
In ΔABC, D and E are the two points of AB and AC respectively,
such that, AD/DB = AE/EC.
To Prove
DE || BC
Proof
In ΔABC,
given, AD/DB = AE/EC ----- (1)
Let us assume that in ΔABC, the point F is an intersect on the side AC.
So we can apply the Thales Theorem, AD/DB = AF/FC ----- (2)
Simplify, in (1) and (2) ==> AE/EC = AF/FC
Add 1 on both sides, ==> (AE/EC) + 1 = (AF/FC) + 1
==> (AE+EC)/EC = (AF+FC)/FC
==> AC/EC = AC/FC
==> EC = FC
From the above, we can say that the points E and F coincide on AC.
i.e., DF coincides with DE.
Since DF is parallel to BC, DE is also parallel BC
Hence the Converse of Basic Proportionality theorem is proved.
SOURCE- EASYCALCULATION.COM
Sunday, 21 July 2013
similarity in triangles
Two geometrical objects are called similar if they both have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or shrinking), possibly with additional translation, rotation and reflection.
This means that either object can be rescaled, repositioned, and
reflected, so as to coincide precisely with the other object. If two
objects are similar, each is congruent to the result of a uniform scaling of the other.
If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure.
This article assumes that a scaling can have a scale factor of 1, so that all congruent shapes are also similar, but some school text books specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different to qualify as similar.
 and
and 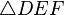 are said to be similar if either of the following equivalent conditions holds:
are said to be similar if either of the following equivalent conditions holds:
1. They have two identical angles, which implies that their angles are all identical. For instance:
 and
and 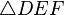 are similar, one writes
are similar, one writes
If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure.
This article assumes that a scaling can have a scale factor of 1, so that all congruent shapes are also similar, but some school text books specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different to qualify as similar.
 | |
| figures with same colours are similar |
Similar triangles
Two triangles and
and 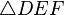 are said to be similar if either of the following equivalent conditions holds:
are said to be similar if either of the following equivalent conditions holds:1. They have two identical angles, which implies that their angles are all identical. For instance:
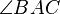 is equal in measure to
is equal in measure to 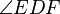 , and
, and  is equal in measure to
is equal in measure to  . This also implies that
. This also implies that  is equal in measure to
is equal in measure to 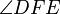 .
.
 . This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other.
. This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other.
 and
and  is equal in measure to
is equal in measure to  .
.
 and
and 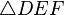 are similar, one writes
are similar, one writesSaturday, 13 July 2013
OGIVES
Cumulative histograms, also known as ogives, are graphs that can be used to determine how many data values lie above or below a particular value in a data set. The cumulative frequency is calculated from a frequency table, by adding each frequency to the total of the frequencies of all data values before it in the data set. The last value for the cumulative frequency will always be equal to the total number of data values, since all frequencies will already have been added to the previous total.
An ogive is drawn by
- plotting the beginning of the first interval at a
 -value of zero;
-value of zero; - plotting the end of every interval at the
 -value equal to the cumulative count for that interval; and
-value equal to the cumulative count for that interval; and - connecting the points on the plot with straight lines.
Example 1: Cumulative frequencies and ogives
Determine the cumulative frequencies of the following grouped data and complete the table below. Use the table to draw an ogive of the data.
| Interval | Frequency | Cumulative frequency |
 | 5 | |
 | 7 | |
 | 12 | |
 | 10 | |
 | 6 |
Solution
To determine the cumulative frequency, we add up the frequencies going down the table. The first cumulative frequency is just the same as the frequency, because we are adding it to zero. The final cumulative frequency is always equal to the sum of all the frequencies. This gives the following table:
| Interval | Frequency | Cumulative frequency |
 | 5 | 5 |
 | 7 | 12 |
 | 12 | 24 |
 | 10 | 34 |
 | 6 | 40 |
The first coordinate in the plot always starts at a  -value of 0 because we always start from a count of zero. So, the first coordinate is at
-value of 0 because we always start from a count of zero. So, the first coordinate is at  — at the beginning of the first interval. The second coordinate is at the end of the first interval (which is also the beginning of the second interval) and at the first cumulative count, so
— at the beginning of the first interval. The second coordinate is at the end of the first interval (which is also the beginning of the second interval) and at the first cumulative count, so  . The third coordinate is at the end of the second interval and at the second cumulative count, namely
. The third coordinate is at the end of the second interval and at the second cumulative count, namely  , and so on.
, and so on.
 -value of 0 because we always start from a count of zero. So, the first coordinate is at
-value of 0 because we always start from a count of zero. So, the first coordinate is at  — at the beginning of the first interval. The second coordinate is at the end of the first interval (which is also the beginning of the second interval) and at the first cumulative count, so
— at the beginning of the first interval. The second coordinate is at the end of the first interval (which is also the beginning of the second interval) and at the first cumulative count, so  . The third coordinate is at the end of the second interval and at the second cumulative count, namely
. The third coordinate is at the end of the second interval and at the second cumulative count, namely  , and so on.
, and so on.
Computing all the coordinates and connecting them with straight lines gives the following ogive.
Ogives do look similar to frequency polygons, which we saw earlier. The most important difference between them is that an ogive is a plot of cumulative values, whereas a frequency polygon is a plot of the values themselves. So, to get from a frequency polygon to an ogive, we would add up the counts as we move from left to right in the graph.
Ogives are useful for determining the median, percentiles and five number summary of data. Remember that the median is simply the value in the middle when we order the data. A quartile is simply a quarter of the way from the beginning or the end of an ordered data set. With an ogive we already know how many data values are above or below a certain point, so it is easy to find the middle or a quarter of the data set.
source- m.everythingmaths.co.za
Subscribe to:
Comments (Atom)